Alla scoperta delle formule per il calcolo dell'area

Percorso didattico per introdurre il concetto di area come misura dell’estensione di una figura, e condurre i bambini alla scoperta delle formule per calcolare l’area delle figure geometriche più semplici (rettangoli, quadrati, parallelogrammi, rombi e triangoli)

Per giungere sin qui abbiamo affrontato la tappa necessaria sulla costruzione del concetto di estensione

per poter passare alla costruzione del concetto di area come misura dell’estensione di una figura ed alla 
scoperta delle formule per calcolare l’area di un rettangolo e poi quella per i parallelogrammi e per i triangoli, attraverso trasformazioni, da loro scoperte, che riconducono l’estensione di quelle figure a quella di un rettangolo

Prerequisiti necessari i concetti di concetti di perpendicolarità, congruenza, equiestensione, misura,  riconoscimento degli elementi di un poligono e conoscenza della relativa nomenclatura (lati, basi, altezze, diagonali)

In una prima fase abbiamo utilizzato come unità di misura il quadretto che però non si è rilevato efficiente in quanto in classe avevamo in uso, sui diversi quaderni, quadretti di varie dimensioni. 

Questo ha fatto nascere la necessità di ricorrere alle unità di misure convenzionali ed in particolare a scoprire le misure di superficie (avendo già affrontato le misure di lunghezza, capacità, peso/massa).

Per comprenderle è stato necessario costruire il nostro campione, il metro quadrato, individuando nel decimetro quadrato la nostra unità di riferimento. Abbiamo scoperto quanti decimetri quadrati ci sarebbero serviti per formare un metro quadrato, riconoscendo nello schema uno schieramento e lo stesso ragionamento lo abbiamo applicato a multipli e sottomultipli.

Il riconoscimento dello schieramento si è ripresentato quando è stato necessario scoprire come si poteva calcolare l'area di un rettangolo che avevamo preso in considerazione. 

Non è stato difficile per i bambini individuare lo schieramento e da lì arrivare a scoprire che per calcolare l’area di un rettangolo basta moltiplicare fra loro le sue dimensioni.

Abbiamo verificato attraverso la costruzione di modelli di carta che la scoperta fosse valida per tutti i rettangoli

Quindi, ricorrendo alla nomenclatura relativa agli elementi di un poligono,

abbiamo tradotto la scoperta in una formula generale

A= b x h 

Nella fase successiva abbiamo applicato lo stesso ragionamento al quadrato. Precisando però che in questo caso la base e l'altezza sono i lati congruenti di un quadrato.

A= l x l

Per il triangolo siamo partiti da un modello di carta di un rettangolo e la scoperta è passata dal ricavare due triangoli, che abbiamo verificato essere congruenti, dal rettangolo di partenza, mediante opportune operazioni di ritaglio e di ricomposizione.

I bambini hanno quindi suggerito di dividere in due parti l'area del rettangolo per scoprire l'area di ogni triangolo.

Ne abbiamo ricavato la formula generale, prima verificata con altri modelli per tutti i triangoli

A= (b x h) : 2

Ora siamo giunti al rombo che abbiamo inscritto sempre all'interno del nostro rettangolo di riferimento,  ottenuto unendo i punti medi dei lati del rettangolo.

Ho chiesto quindi come potevamo questa volta ragionare per poter calcolare l'area di quel rombo.

Abbiamo tagliato i triangoli al di fuori del nostro rombo che sovrapposti al rombo inscritto sono risultati ricoprirlo tutto perfettamente, dunque formare un secondo rombo congruente al primo.

E di nuovo passare dalla scoperta ad una formula generale ai bambini è sembrato facile.

Questa volta però abbiamo fatto riferimento alla nomenclatura relativa al rombo e richiamato alla mente una scoperta precedente, ossia che le diagonali maggiore e minore del rombo sono congruenti alla base ed all'altezza del rettangolo di partenza.

Dunque invece di riferirci nella formula a base e altezza del rettangolo, dovevamo riferirci a diagonale maggiore e minore del rombo.

A= (D x d) : 2

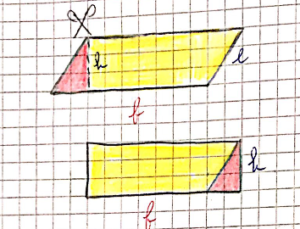
Romboide

Partendo dal nostro rettangolo tracciamo il segmento che unisce un vertice del rettangolo con un punto della base, trasliamo il triangolo ottenuto sul lato opposto del rettangolo ed otteniamo un romboide che conserverà la stessa misura dell'area del rettangolo da cui lo abbiamo ottenuto.

Dunque la formula sarà la medesima 

A = b x h

Le varie tappe del percorso didattico di quest'anno documentate sul blog

https://classeacolori.blogspot.com/search/label/matematica?&max-results=7