Calcolo, addizioni con passaggio alla decina

"La consapevolezza che ogni numero si può esprimere come somma di altri due numeri in molti modi diversi, e il sapere individuare la totalità di queste coppie additive, costituiscono delle acquisizioni decisive per poter pensare e operare con i numeri. In particolare la memorizzazione ragionata di tutte le diverse coppie additive del dieci, rappresenta uno strumento nel calcolo di addizioni e sottrazioni, non meno importante di quello rappresentato dalle tabelline per la moltiplicazione". 

(CIDI Percorso IL NUMERO IN PRIMA ELEMENTARE)

Durante il nostro percorso in classe prima ci siamo soffermati con attenzione sulle coppie additive di 10.

Conoscere le coppie additive di 10 

• costituisce la base per sviluppare il calcolo a mente che sfrutta strategie di manipolazione della numerosità e tutti i meccanismi dell’intelligenza numerica e del ragionamento in essi implicato; 
• permette di rielaborare le operazioni di addizione e di sottrazione in una forma più semplice.

Costituisce un passaggio delicato calcolare somme passando dalla decina.
Per riuscire è necessario:

• saper eseguire addizioni in riga;
• conoscere le coppie additive del 10;
• saper scomporre numeri.

Sappiamo  che:

«Le principali strategie del calcolo a mente identificate dalla letteratura scientifica sono: 

• Counting all e counting on: : il contare da un certo numero in poi è un passaggio di qualità rilevante nell’uso delle strategie in quanto indica la capacità del bambino di operare con i numeri, l’inizio della costruzione del sistema di calcolo; 

• Raggruppamento (più unità alla volta): è la strategia che aiuta i bambini a trovare punti di riferimento per calcolare in modo facile, un esempio è il 5 che semplifica il calcolo; 

• Arrotondamento alla decina: rappresenta una forma evoluta delle strategie di raggruppamento, 

es 8+7 → 8+2+5 

• Composizione e scomposizione del numero: sono le strategie più flessibili nell’uso. Il numero viene scomposto nel modo migliore per facilitare il calcolo utilizzando contemporaneamente le strategie di arrotondamento alla decina e/o altri tipi di raggruppamenti più funzionali al calcolo: 

43+15→ (43+5) + 10 

• Recupero dei fatti aritmetici: strategia veloce ed economica, chiaro indice dell’automatizzazione del calcolo». 

Sviluppare l’intelligenza numerica 2 – D. Lucangeli, S. Poli, A. Molin - Erickson

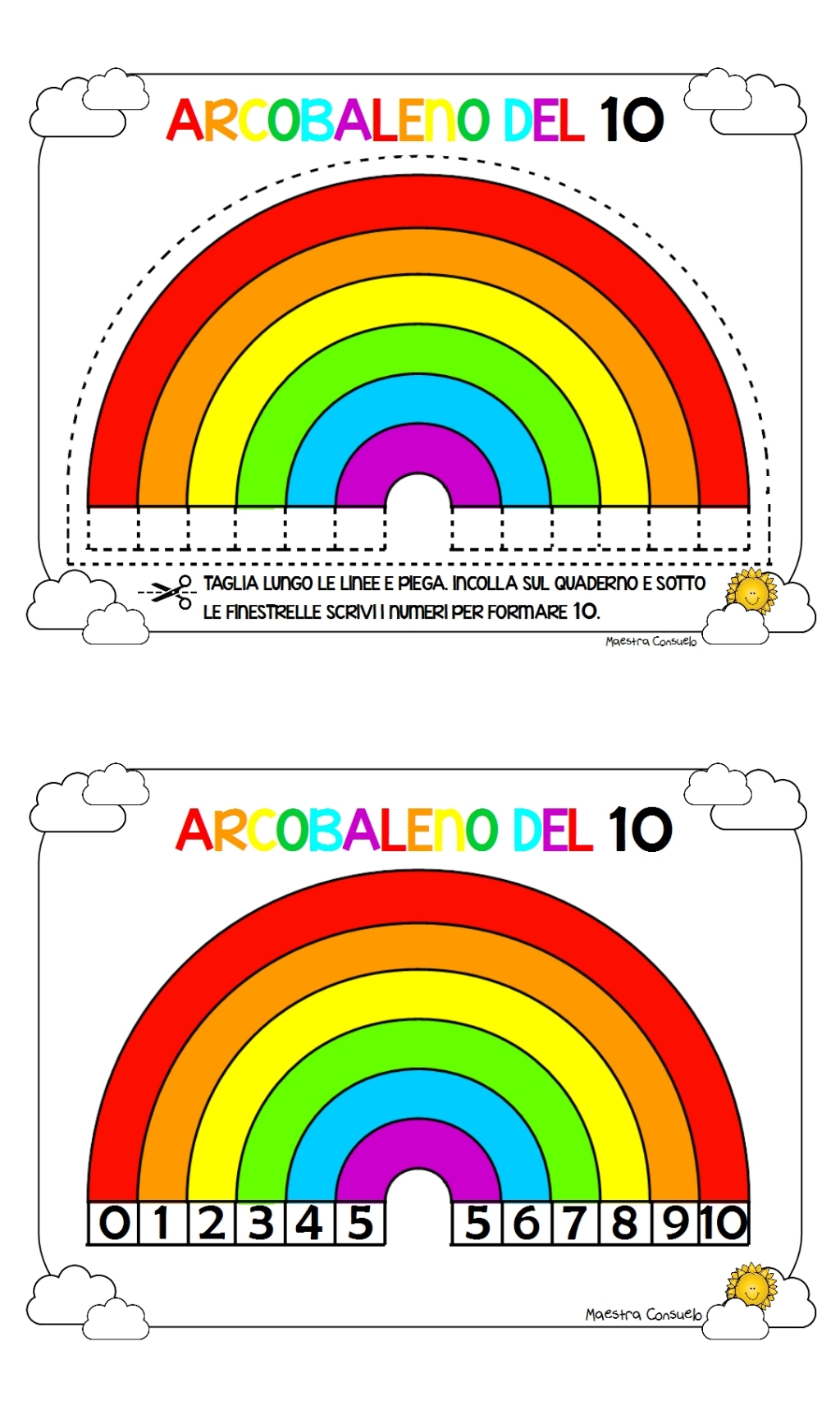
Cominciamo con esempi più semplici eseguiamoli tutti insieme aiutandoci con le dita (dita alzate e abbassate) con la costruzione dell'arcobaleno del 10, con la linea dei numeri

Il materiale condiviso da Maestra Consuelo su www.freeed.com

Poi passiamo al ragionamento nello svolgimento di una addizione

Addizione 6 + 7 = 

devo scomporre 7 in una coppia di numeri: il primo numero deve far parte della coppia additiva di 6 per formare 10

Chi è l'amico di 6? risposta 4

Allora il primo dei due numeri sarà 4
Se ho 4 dita sollevate, quante dita devo ancora alzare per formare 7? risposta 3

Allora la coppia sarà 4,3

         7
6 + 4 + 3

6 + 4 formano 10 ---> 10 + 3 = 13

Addizione 7 + 8 =
devo scomporre 8 in una coppia di numeri: il primo numero deve far parte della coppia additiva  di 7 per formare 10
Chi è l'amico di 7? risposta 3
Allora il primo dei due numeri sarà 3
Se ho 3 dita sollevate, quante dita devo ancora alzare per formare 8? risposta 5

Allora la coppia sarà 3,5

         8
7 + 3 + 5

7 + 3 formano 10 ---> 10 + 5 = 15

Potremmo poi passare, all'interno delle attività di potenziamento, ad esempi con il passaggio alle decine successive:
il ragionamento è il medesimo

1. individuare il numero della coppia che mi fa arrivare alla decina successiva;
2. scomporre il secondo addendo in una coppia numerica che per primo ha il numero che permette di raggiungere la decina successiva e per secondo il numero che manca per formare il secondo addendo (es. 5 = 2 + 3 , dove 2 con 18 forma la decina successiva - 20 - invece 3 sono le dita che devo alzare per formare 5);
3. eseguire il calcolo.

Anche nel caso dei numeri entro la seconda decina si può preparare un arcobaleno e fare con i bambini le dovute osservazioni scoprendo che sono ancora le coppie additive del 10 che ci aiuteranno a raggiungere sempre il numero venti (decina successiva)

Barbara Battistini

👀https://www.youtube.com/watch?v=D2vLH2NDz64

Ed ora giochi on line sulle addizioni e sottrazioni entro il 20👇

• https://www.giochidimatematica.it/addizioni-fino-a-20/
• https://www.giochidimatematica.it/sottrazioni-fino-a-20/
• https://www.matific.com/it/it/home/maths/episode/hopping-on-the-number-line/?grade=grade-1
• https://www.matific.com/it/it/home/maths/episode/hop-on-the-bus-use-counting-to-add-and-subtract-whole-numbers/?grade=grade-1
• https://www.matific.com/it/it/home/maths/episode/cherry-chomp-solve-subtraction-from-20/?grade=grade-1

Altri giochi per la classe prima

Matika.in